汉诺塔

Posted on | In

汉诺塔的递归学习

汉诺塔

汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。—百度百科

汉诺塔模型

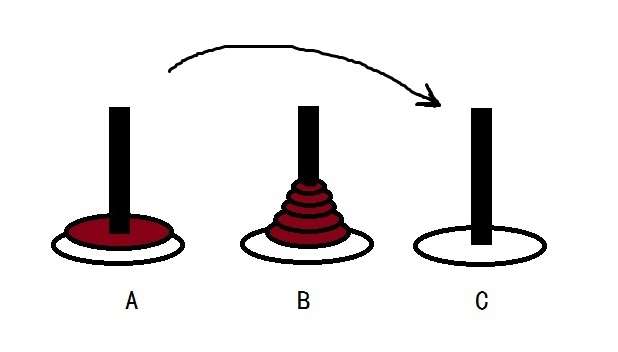
递归思想

https://www.zhihu.com/question/24385418
（参考知乎提问的答案）

阅读后理解

阅读知乎回答后的理解，假设有1 2，3个盘子， 质量按照数字大小区分，参考了YIHE陳的回答，其中间状态就是，我们必须要把最大的那块，先放到Ｃ柱，才能往后走（因为大盘子必须在小盘子下面），如果要把最大那块放到C柱，那么1、2两块的位置必须先在B中暂存，假设已经到了这一步，下一步就是把3放到C中，ok，那么B此时与刚开始的A柱的情况是一样的，C中的3可以忽略，因为最大的必须在最下面，他无法去在1、2上面，那么在B中，又套用一次之前放3的方法，即可完成整个流程
初始状态

1
2
3
A [1,2,3]
B []
C []

中间状态

1
2
3
A[3]
B[1,2]
C[]

完成一次最大块转移后

1
2
3
A[]
B[1,2]
C[3]

这时，把B的[1,2] 还给A，跟初始状态一样 

1
2
3
4
A（B）[1，2]
B（A）[]
C[3]
这时再走一次上面的方法

有点像这个图(原图出自知乎回答)




数学推导

{
Hn=2 * Hn-1 + 1 ?== 2^n -1
H1=1
}
证明如下图

代码实现

Python版本

1
2
3
4
5
6
7
8
9
10
def move(n, a, b, c):
    if n == 1:
        print(a, '-->', c)
    else:
        move(n - 1, a, c, b)  #放到b中
        move(1, a, b, c)  #
        move(n - 1, b, a, c)# b的盘子换到a的位置


move(3, 'A', 'B', 'C')